
The take home lesson is that the pattern of currents in a body of water is a vastly more complex kind of data that the water levels at its surface.
| A level is a number, which is called a scalar. To completely describe the water level over a large body of water it is necessary to give the level at several locations, because the tide is not high or low at the same time at different locations, and the tidal range is different at different locations. In practice, the locations for which the tides are measured and predicted are usually harbors or locations of importance for shipping or fishing. However, a complete tidal prediction would consist of a chart with water levels indicated at regularly spaced intervals. Thus, water levels are scalars defined on a two dimensional plane. | |||||||
 |
|||||||
 |
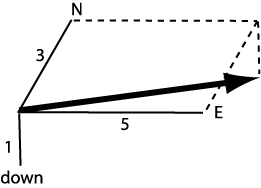
A current is not just a number. A current has a speed and a direction, and it takes three numbers to describe this kind of data, which is called a vector. The most common (but not the only) way to describe a vector is to give the velocity in three reference directions that are perpendicular to each other. To describe a water current it might be natural to use North, East, and down as the three reference directions. Then a current, the arrow in the diagram, would be described by giving the velocity components along these three directions. The current in the diagram would then be described as (3,5,1) if the convention is to give the N, E, down components in that order. It is not important which directions are used as the references, or the order in which the components are given. It is only important for the convention to be clearly stated, so the interpretation of the three numbers is unambiguous. | ||||||
| Currents are defined throughout a body of water, not just at the surface. Thus, a complete description of currents in a body of water consists of vectors distributed in all three directions, not just on the two dimensional surface of the water.
The take home lesson is that the pattern of currents in a body of water is a vastly more complex kind of data that the water levels at its surface. |
 |
||||||