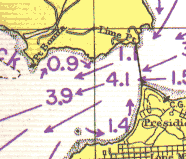
A current flowing past a cove usually induces a circular current in that cove. The two Figures on the right, from the NOAA current charts, show the water just outside the Golden Gate Bridge (the straight vertical line just to the right of the center). For scale, the length of the Bridge is approximately one mile.

One vortex is in Bonita Cove, on the North (upper) shore, just to the right of Pt. Bonita. The other vortex is in South Cove, on the South (lower) shore, just to the left of the bridge.

The first Figure is one hour after maximum flood at the San Francisco Bay entrance. The current in the middle of the Entrance is 3.0 knots, while the counter current in Bonito Cove is 1.1 knots and in South Cove 0.9 knots.

The second Figure is one hour after maximum ebb at the Entrance. The current in the middle of the Entrance is 4.1 knots, while the counter current in Bonita Cove is 0.9 knots and in South Cove is 1.4 knots.

In these two coves a counter current is obvious because the net current is opposite in direction to the main current. In many other locations the same types of forces generate a counter current component that is not sufficiently strong to reverse the net current. In these locations the counter current component can only be discerned by the fact that the average current is far from zero.

Another example is China Cove, on the North-East end of Angel Island. This little cove is only about 50 feet deep and 200 feet long, but it also induces a circulating current, as illustrated in the picture on the left (currents were estimated by the author as motion of patches of foam on the waters surface) . The point of land that forms the right side of the cove also generates turbulence as the current splits into two arms.

Importance to a rower

If you are rowing with the current along a shore you may encounter a counter current and thus lose time if you go into a cove. However, if you are rowing against the current, it may be worth a distance penalty to go into a cove and pick up a counter current.

Both the time of high tide, and the actual height of the tide at its highest, vary with location throughout the Bay. Thus, the surface of the water is never completely level. One possible theory for tidal currents would be that they are solely a response to these differences, i.e. water always runs down hill. Thus, a current is just the flow of water from a higher to a lower location. However, you can never generate a circular current, a vortex, with such a model, since there is no way you can start at one point, move along a curve that brings you back to the same location, and go downhill all the way. As is seen in the Figure to the right, when you return to the starting point you will always return also to the same level. Differences in water level are certainly an important force in causing currents but there are other factors that influence current velocity.

In mathspeak: Since curl grad V = 0, any vector field that has a non-zero curl can not be a gradient of a scalar field.