You are sitting on a dock on the bank of a small lake just before sunset. It's the time when there is no wind, and the lake is calm, very calm. The light hits the water at a flat angle, so you can see the slightest disturbance of the surface. The water is flat.
Then you feel the slightest breeze on you cheek, and it continues for some time. Never the less, the water is flat. After a while the wind freshens, and finally you see ripples on the water. As the breeze turns into a blow, the waves become higher and the distance between the waves becomes longer. What's going on here? Is it interesting?
I think it's interesting, or I wouldn't be writing this (also see).

First, look closely at the surface of the water before the wind comes up. It appears flat, but a very close inspection reveals a complex collection of very small waves moving at different speeds in different directions. How small the waves are depends on the environment, but there are always some disturbing forces, animals, sound, leaves falling in the water, anything.
There will be a few waves moving in the direction of the wind. The wind will transfer the most energy to these waves, and they will grow in size and finally move almost as fast as the wind. Gradually these waves will dominate the surface profile of the water, as seen in the diagram to the right. You can think of this process as evolution and selection.
Wait, what do we hope to learn?
I hope your interest in waves has been wetted, but we need to be a little realistic about what we plan to discuss in this tiny essay. There are so many things about waves that are interesting. For example, there are hundreds of papers just on the process described above, the interaction of wind with water. There are also many layers to understanding waves, but most of them require familiarity with advanced mathematical concepts. Here our goal must thus be modest: the relationship between wavelength and speed for wind driven water waves.
This may seem a little too modest a goal. However, I will try to convince you that, while not the Holy Grail, it is still worth some effort. As in many quests, we will learn some unexpected things in our search.
1. Disturbing forces: We described above the one we are interested in, the force due to wind interacting with the water surface. This can be complicated, but all we say about it here is that for the wind to put energy into the waves they must be moving slightly slower than the wind. If the waves are moving faster they will instead loose energy to the air.
2. Restoring forces: There must be at least one force that pushes or pulls the water surface back to its original flat position, otherwise we won't have waves, the water will just fly out of the lake. The first restoring force is obvious:
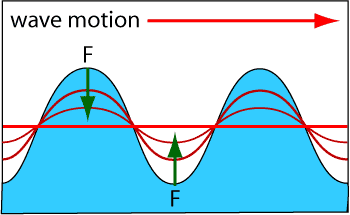
Some portions of the blue water on the left are above, and some are below the resting level of the water. Gravity forces the higher water down and the lower up, as indicated by the green arrows. How gravity can force water up will be discussed later.
Wait: If that is all that was going on, the surface of the water will just go up and down to generate waves like the other two red curves in the above diagram. These waves don't move, they just go up and down. Such waves do exist and they are called "standing waves" . Great, but we want waves that move to the right with the wind. How gravity can force water up from the trough of the wave to the resting level will be described later.
Gravity:
F = g d
F: force per unit volume
g: gravitational force per unit mass
d: the density of the water or mass per unit volume
Surface tension:
F = T curvature
F: force per unit length at surface
T: surface tension of the water
curvature: the second derivative of the surface; how rapidly the surface bends
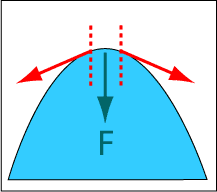
Water molecules are attracted and bonded to each other by hydrogen bonds. However, at an air-water surface each water molecule can only bond to water below it. The overall effect is a force to minimize the total surface area. Mathematically this is equivalent to a force proportional to the second derivative of the surface. It is as if the water surface was a thin sheet of stretched rubber. If the left and right edges of the surface in this diagram were fixed, surface tension (the red arrows) would tend to flatten the surface (the green arrow).
3. Inertial and mass conservation forces: It may seem strange to group these two internal forces together, but it won't change the physics, so here goes.
By inertial forces I refer to Newton's basic law that says objects move at a constant velocity unless a force is applied. The force required per change in velocity (acceleration) is proportional to the mass.
F = m a
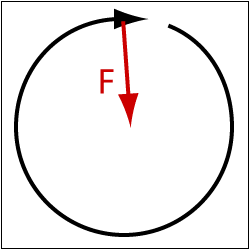
A change in velocity can mean a change in speed or a change in direction. A simple example of a change in direction is an object moving in a circle, as on the left diagram. The velocity is constantly changing toward the center so a force toward the center is required. Of course this is just the situation when the earth revolves around the sun; the force is the force of gravity between the earth and sun. It also turns out to be the situation when a water wave moves to the left (see below).
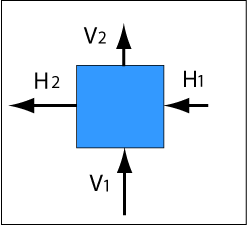
By conservation forces I mean pressures that maintain balanced flows. Balanced flows ensure the amount of water flowing into a region equals the amount flowing out; water is neither created or destroyed. This principle is also called conservation of mass.
Imagine that the water is divided into many imaginary squares (we assume there is no flow in the plane of the diagram) so we can do the book keeping. On the left there are horizontal (H) and vertical (V) flows. In the horizontal direction the flow in on the right, H1, is less than the flow out on the left, H2. The resulting loss of water must be balanced by an increase from vertical flows V1 and V2.
H1 - H2 = V1 - V2
It is this system of pressures that allow the downward force of gravity on the crest of waves to also force the water in the troughs upward, as seen in a previous diagram. The water in the crests is connected to the water in the troughs.
4. Dissipative forces: As internal currents in water flow past each other, and as the water flows over the bottom and sides of the lake (or river, ocean, bay, or whatever) energy is lost due to molecular friction. The loss of energy is proportional to the viscosity of the water. If the wind should stop suddenly, the waves will gradually decrease in size and the lake will become calm again. This is reassuring, but we will not pursue this process any further here.
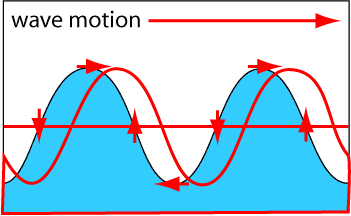
In the diagram on the right we have a wave moving to the right (blue wave moving to the red wave). An obvious way for this to occur would be for all the water to just move to the right, transforming the blue to the red curve. But, as anyone who has been in a boat knows, this isn't what happens when a train of waves passes under you. The entire water isn't moving with the wave, instead it just feels like you are going up and down with the waves.
Actually, in the boat you are going up and down and left to right. This is because the water at each point moves in a circle; the small red arrows show the velocity of the water at each part of the wave cycle. One take home lesson here is that calculation of the velocities is a little complex, and requires some maths.
Using these forces the velocities of water in a wave traveling at constant speed to the right can be found. Below I give you a bonus (because I said all we would learn is the relationship between the velocity of the wave and its length ), the movement of water at various parts of the wave.
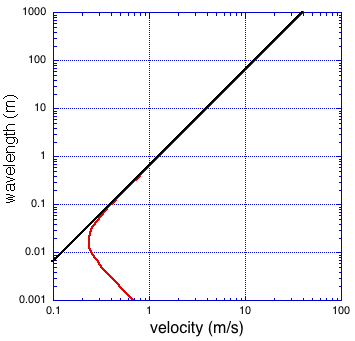
Now, what I promised, speed versus wave length (as an approximation good for deep water):
v2 = [g L / 2 pi] + [2 pi T / d L]
where pi = 3.14159..., g = gravity constant,
L length, T surface tension, d density
I consider the velocity the independent variable, plotted on the horizontal axis, because it is defined by the wind. The wave length is the response of the water to the wind.
I have used a log-log plot only because I want to show a wide range of velocity values. To give the metric impaired a feeling of scale, 1 m is about one yard and 1 m/s is 3600 m/hr or 3.6 km/hr or 2.2 mph.
The straight black line is the response if the surface tension were zero, while the red line is the response for clean water.
Look closely at the equation and its curve and behold!
First, for clean water there is a minimum velocity for water waves; the bend in the red curve. Thus, as suggested in the very first paragraph of this essay, winds with velocities less than 0.23 m/s can't make waves.
You can also see this from the equation, since for small L the second term becomes large while for large L the first term is large; there is no L where v becomes zero. Since the first term is due to gravity, and the second depends on surface tension, another way to state this is: long waves move fast using gravity while short waves move fast using surface tension. This is a specific example of a very important principle: the forces that are important depend on the size scale of interest.
Secondly, for any wind that can make waves, there will be two wavelengths. However, at velocities above 1m/s the wave lengths of the small waves become quite small (less than 1 mm).

The ripples rely on surface tension of the water, while the large wave uses gravity as the restoring force.
I have used the phrase "clean water" several times when mentioning surface tension waves. That is because the value for the surface tension of water is very dependent on the surface being water, not oil or protein or soap or anything else. It takes a very small amount of any material which floats, oil for example, to produce a film one molecule thick on the surface. The surface of the ocean is never (well hardly ever) water, there are to many living and dead organisms in the ocean, thus too high a concentration of oils, proteins, etc.