Models made of pools are used in many fields other than pharmacokinetics, e.g. biology, chemistry, meteorology, and economics. One example from the field of biochemistry is a study using radioactive phosphorous to measure the length of RNA in bacteria. RNA is a polymer of nucleotides which is copied from genes in DNA and enables synthesis of proteins. One class of RNA actually codes the amino acid sequences of proteins, and is thus called messenger RNA, or mRNA.
	mRNA chains are at least several thousand nucleotides long. There are several methods to physically measure the length of an RNA chain. However, mRNA in bacteria has a life span of only a few minutes before it is degraded back into the nucleotide building blocks it was made from. The RNA chains are made by sequentially adding nucleotides to the growing chain at a rate of about 50 per second, and the breakdown of many longer chains starts before they are finished. Fortunately, the first nucleotide of the RNA chain retains the three phosphates of the nucleotide triphosphate building block, while the remaining nucleotide triphosphates loose two phosphates as they are added to the growing chain (it is the loss of these phosphates that provides the energy to drive the synthesis). It is fairly easy to isolate radioactivity labeled RNA, degrade it chemically into single nucleotides in a way that preserves the three phosphates of the first nucleotide, and separate nucleotides with one, and nucleotides with three phosphates. If we then just measure the ratio of radioactivity in monophosphate to triphosphate nucleotides, we will have the length (note that breaks in the middle of RNA chains will not hurt us, because the ends of these breaks will not have three phosphates as do the "real" ends).

	A serious complication is indicated by the two colors used to represent the phosphates (the little red and orange circles) of the RNA. After the radioactive phosphorous is added to the bacterial culture, the two end phosphate groups on RNA become radioactive quickly, while the phosphates attached directly to the nucleotides, those in the interior of the chains, becomes labeled much more slowly. Thus, when you isolate RNA, the end phosphates have more activity per molecule than the interior phosphates. The ratio of radioactivity does not give us the length. The cause of unequal labeling is seen in diagram to the right, showing the mono-tri-mono phosphate cycle. Nucleotide monophosphates are converted to triphosphates to store energy, as for example sugar is burned to CO2. Then triphosphates are converted back to monophosphates as the energy is used for all the needs of the bacterium, with RNA synthesis being one of many reactions. This turnover is far more rapid than the synthesis of new nucleotides, which is the only way for the first phosphate to become labeled with the radioactive isotope. There is no easy way around this problem. We need to isolate nucleotide triphosphates several times after radioactive phosphate has been added to the bacterial culture, and determine the relative amount of isotope in each of the three phosphates.

			Determination of the relative amount of radioactivity in the phosphates is incredibly time consuming (you don't want to know the details). We can only afford a few time points, but we want to know the relative radioactivity over the complete time span of the experiment. A pool model is the solution. In pharmacokinetic models a pool is a physical compartment, and transport is flow between compartments. In the radioactive labeling case a pool is a single species of nucleotide, and transport between pools represents the chemical reaction that converts one form to the other. The math is the same. 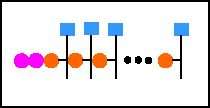The raw kinetics of isotope incorporation (counts per minute, cpm) into interior (orange) and terminal (red) nucleotides, top panel, left figure, are nonlinear, with different shapes for each. The ratio between interior and terminal thus changes with time after isotope addition, about 10 percent at 20 seconds, and 0.2 percent at 5 minutes. We can convert to absolute amounts, e.g. nanomoles (n moles) knowing the relative activities of the nucleotides. Now the two curves, in the lower panel, are linear with time. This just indicates that RNA is being made at a constant rate. The ratio is also a constant, indicating an average length of about 6000 nucleotides.

The Kinetics of Phosphate Incorporation into ATP and GTP in Bacteria. Lutkenhaus J, Ryan J, Konrad MW, J Bact 116:1113-1123 (1973)

Apparent Average Length of the Transcripional Unit in Bacteria. Konrad MW, J Bact 119:228-241 (1974)